Spoiler alert: This post contains spoilers for Project Euler.
Problem 15
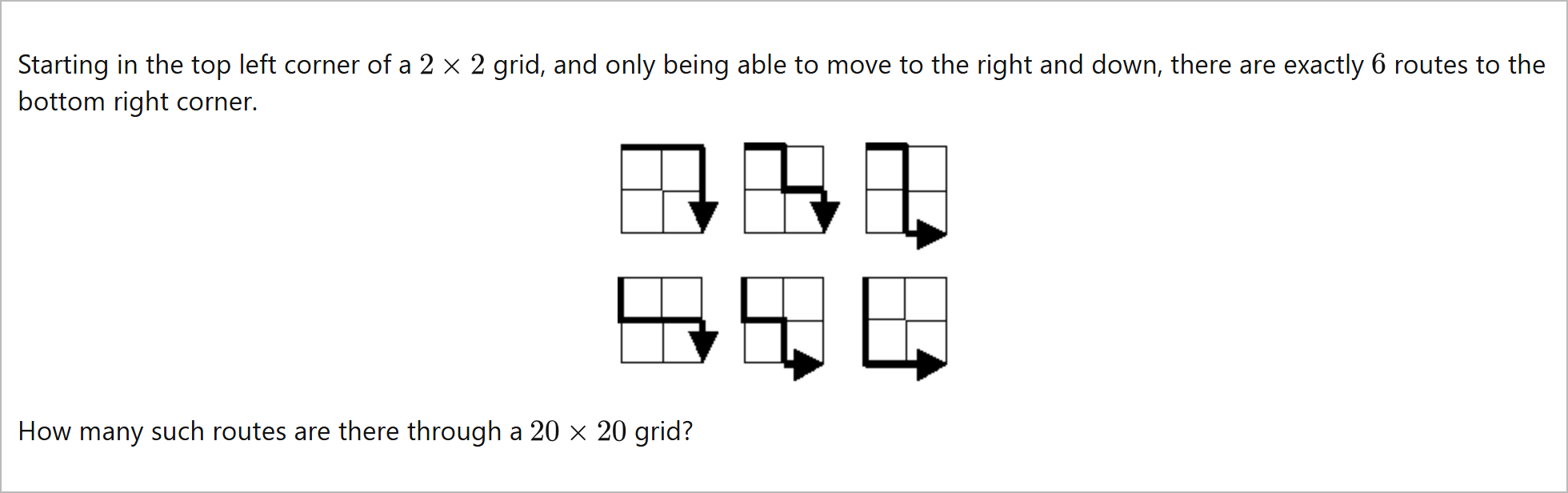
 Lattice Paths
Lattice Paths
Approach
This one took me a lot longer than I first expected. We can easily count the number of routes of a 1x1 and 3x3 grid in addition to the provided 2x2 grid. But counting the routes on a 4x4 or larger grid gets cumbersome very quickly. Doing this manually is error prone. I developed a react component that will generate an .svg for each possible path. This prevents mistakes but also illustrates how quickly the number of routes explodes.
1x1 grid
A 1x1 grid has 2 paths2x2 grid
A 2x2 grid has 6 paths3x3 grid
A 3x3 grid has 20 paths4x4 grid
A 4x4 grid has 70 paths5x5 grid
A 5x5 grid has 252 pathsTrying to Understand the Pattern
My initial difficult is that I didn't want to brute force this. But I also didn't see a clear pattern in the numbers.
| Grid size | # of Routes |
|---|---|
| 1x1 | 2 |
| 2x2 | 6 |
| 3x3 | 20 |
| 4x4 | 70 |
| 5x5 | 252 |
At first glance, it looks like the next number in the series is roughly 3x as large, plus some variable amount. But this is a dead end since that variable amount increases in a way that doesn't have a clear pattern.
| Grid size | # of Routes | 3x # of Routes | Unexplained Remainder |
|---|---|---|---|
| 1x1 | 2 | 6 | 0 |
| 2x2 | 6 | 18 | 2 |
| 3x3 | 20 | 60 | 10 |
| 4x4 | 70 | 210 | The answer to life |
| 5x5 | 252 | - | - |
Realizing This Is An nCr Problem
The length of a route is twice as large as the grid size. For a 2x2 grid, the length is 4. For a 3x3, the length is 6.
When building a route your decisions are restricted. At any point you can choose to go right or down, but not both. The number of choices that you make is limited to the size of the grid. For instance, on a 3x3 grid, I can choose to go right 3 times. But then I must go down 3 times. That is, moving down 3 times is forced.
Really the key insight here was the word "choice". We learned the nCr and nPr functions on our calculators in middle school. With nCr verbally representing "n choose r".
We can just use a calculator for this.
I would have resorted (tried) to brute forcing the answer if I hadn't made this connection.
| Grid size (r) | Route length (n) | nCr |
|---|---|---|
| 1x1 | 2 | 2 |
| 2x2 | 4 | 6 |
| 3x3 | 6 | 20 |
| 4x4 | 8 | 70 |
| 5x5 | 10 | 252 |
| ⋮ | ⋮ | ⋮ |
| 20x20 | 40 | 137,846,528,820 |
Conclusion
It took me a while to make the combinatorics connection - I am glad I didn't try to brute force the answer.